Semejanzas

-Origen de las Semejanzas: Es la variación en tamaño de dos objetos o cuerpos pero sus formas son identificas,se dice que dos figuras geométricas son semejantes si tienen la misma forma pero sus tamaños son diferentes.


¿Que son las semejanzas?:En esta sección se analizara el concepto de semejanza de triángulos con el fin de poder comprender su significado y aplicarlo en la solución de problemas antes de profundizar el concepto se interiorizara solamente el concepto de semejanza.



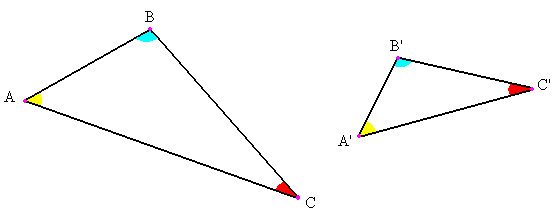
Para lo que se quiere realizar,es necesario el conocimiento de los que son lados correspondieres y lo que es proporcionalidad para ello considere la figura que se muestra abajo en la que los lados correspondientes son respectivamente
 
                                              c y c' (lado grande y lado grande)                                             a y a' (lado pequeño y lado pequeño)                                             b y b' (lado mediano y lado mediano)




Observe se que al realizar la división entre los lados homólogos (correspondientes) el resultado que se obtiene  es 2 (dividiendo 10 entre 5, 8 entre 4 y 6 entre 3), este valor recibe el nombre de razón y cuando la razón es igual en todos y cada uno de los lados correspondientes, se dice que los lados son proporcionales.

El concepto de semejanza en la vida cotidiana

Cuando se utiliza el término de semejanza en el lenguaje cotidiano, ¿a qué nos estamos refiriendo?  Será acaso:

• Un objeto que se parece a otro
• Objetos de igual tamaño
• Objetos de igual forma
• Objetos exactamente iguales
  El concepto de semejanza en matemática
  El concepto de semejanza en matemática está muy ligado al concepto de proporcionalidad.  En esta ciencia se dice que dos objetos son semejantes si "guardan" una proporción entre ellos.  Veamos algunos ejemplos de la relación existente entre semejanza y proporcionalidad.
  1. Un geógrafo desea determinar la distancia entre dos ciudades, para ello utiliza un mapa.  Se percata que la escala utilizada en el mapa es de 1:5000, es decir, un centímetro en el mapa representa 5000 metros en la realidad.  Luego de medir con una regla la distancia entre las dos ciudades, obtiene que es de 3cm, lo cual representa 15000 metros en la realidad.  Note que el mapa es una representación semejante a una porción del globo terráqueo, de allí que, deba guardar una misma proporción, con el fin de que las medidas que se tomen sobre él sean lo más cercanas a su valor real. 
  2. La construcción de modelos a escala (aviones, barcos y edificios, entre otros) requiere de una buena aplicación de los conceptos de semejanza y proporcionalidad, esto con el fin de que la maqueta sea lo más semejante posible al objeto real, además de guardar una proporcionalidad adecuada, en otras palabras, el tamaño de cada una de sus partes debe estar acorde con el tamaño que el objeto tiene en la realidad.
  3. Dos fotografías de la misma persona, una de tamaño 3x4 pulgadas que luego es ampliada a 6x8 pulgadas.  Ambas son semejantes y tienen una misma proporción, ya que una es la ampliación de la otra tanto a lo ancho como a lo largo y con una misma razón, o sea, las divisiones de sus lados correspondientes son de igual valor.
  4. Dos anillos idénticos, cuyos diámetros son exactamente iguales, guardan la misma proporción y semejanza entre cada una de sus partes (circunferencia, radio, área, diámetro).
  El último ejemplo refleja que siempre, dos objetos que son del mismo tamaño y forma se pueden catalogar como semejantes.  Se debe tener cuidado con la afirmación inversa, es decir, objetos de diferente tamaño no son siempre semejantes, todo depende de que guarden o no la misma proporción, tal es el caso de los ejemplos uno, dos y tres.   En otras palabras, para que dos objetos sean semejantes bajo la concepción matemática, no siempre tienen que ser iguales.
  Resumiendo:  dos figuras son semejantes si guardan una proporción entre cada una de sus partes respectivas.
  
  Aquí les dejaremos un vídeo sobre las semejanzas:
  
  

          Física:

- Movimiento Rectilíneo Uniforme: Un movimiento es rectilíneo cuando un objeto describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Es indicado mediante el acrónimo MRU, aunque en algunos países es MRC, por movimiento rectilíneo constante.

- Movimiento Rectilíneo Uniformemente Acelerado: Movimiento de trayectoria rectilínea y velocidad variable, con aceleración constante (uniformemente acelerado). Si la velocidad aumenta a lo largo del tiempo, la aceleración se considera positiva. Si la velocidad disminuye a lo largo del tiempo, la aceleración es negativa (movimiento desacelerado, decelarado o de frenado).

- Dinámica: es la parte de la Física que estudia el movimiento de los cuerpos y las fuerzas que producen dicho movimiento.

Movimiento Rectilíneo Uniforme

El movimiento rectilíneo uniforme (MRU) fue definido, por primera vez, por Galileo en los siguientes términos: "Por movimiento igual o uniforme entiendo aquél en el que los espacios recorridos por un móvil en tiempos iguales, tómense como se tomen, resultan iguales entre sí", o, dicho de otro modo, es un movimiento de velocidad v constante.

El MRU se caracteriza por:

a) Movimiento que se realiza en una sola dirección en el eje horizontal.

b) Velocidad constante; implica magnitud, sentido y dirección inalterables.

c) La magnitud de la velocidad recibe el nombre de rapidez. Este movimiento no presenta aceleración (aceleración = 0).

El movimiento rectilíneo uniforme se caracteriza porque su trayectoria es una línea recta y el módulo, la dirección y el sentido de la velocidad permanecen constantes en el tiempo. En consecuencia, no existe aceleración, ya que la aceleración tangencial es nula, puesto que el módulo de la velocidad es constante, y la aceleración normal es nula porque la dirección de la velocidad es constante.

La ecuación de la posición para un móvil que se desplaza con un movimiento rectilíneo y uniforme con una velocidad v es:

x = x0 + v·t

Donde x0 es la posición del móvil en el instante inicial. Por tanto, el móvil recorre espacios iguales en tiempos iguales.

También forma parte de la cinemática que se ocupa de la descripción del movimiento sin tener en cuenta sus causas. La velocidad (la tasa de variación de la posición) se define como la distancia recorrida dividida entre el intervalo de tiempo. La magnitud de la velocidad se denomina celeridad, y puede medirse en unidades como kilómetros por hora, metros por segundo. La aceleración se define como la tasa de variación de la velocidad: el cambio de la velocidad dividido entre el tiempo en que se produce. Por tanto, la aceleración tiene magnitud, dirección y sentido, y se mide en unidades del tipo metros por segundo cada segundo.

MOVIMIENTO RECTILÍNEO UNIFORME ACELERADO:El movimiento rectilíneo uniformemente acelerado es un tipo de movimiento frecuente en la naturaleza. Una bola que rueda por un plano inclinado o una piedra que cae en el vacío desde lo alto de un edificio son cuerpos que se mueven ganando velocidad con el tiempo de un modo aproximadamente uniforme; es decir, con una aceleración constante.

Este es el significado del movimiento uniformemente acelerado, el cual “en tiempos iguales, adquiere iguales incrementos de rapidez”.

En este tipo de movimiento sobre la partícula u objeto actúa una fuerza que puede ser externa o interna.

En este movimiento la velocidad es variable, nunca permanece constante; lo que si es constante es la aceleración.

Entenderemos como aceleración la variación de la velocidad con respecto al tiempo. Pudiendo ser este cambio en la magnitud(rapidez), en la dirección o en ambos.

Las variables que entran en juego (con sus respectivas unidades de medida) al estudiar este tipo de movimiento son:

Velocidad inicial           Vo (m/s)

Velocidad final              Vf  (m/s)

Aceleración                     a  (m/s²)

Tiempo                             t   (s)

Distancia                         d  (m)

Para efectuar  cálculos que permitan resolver problemas usaremos las siguientes fórmulas:

Consejos o datos para resolver problemas:

La primera condición será obtener los valores numéricos de tres de las cinco variables. Definir la ecuación que refleje esas tres variables. Despejar y resolver numéricamente la variable desconocida.

Tener cuidado con que en algunas ocasiones un dato puede venir disfrazado; por ejemplo:

"un móvil que parte del reposo.....", significa que su velocidad inicial es Vo = 0 ; "en una prueba de frenado...", significa que su velocidad final es Vf = 0.


MOVIMIENTO RECTILÍNEO UNIFORME EN EL DÍA A DÍA: Encontrar el m.r.u.a en tu día a día es bastante común un objeto que dejas caer y no encuentra un obstáculo en su camino(caída libre)





MOVIMIENTO RECTILÍNEO UNIFORME ACELERADO


-EJERCICIOS: En dirección hacia el sur, un tren viaja inicialmente a 16m/s; si recibe una aceleración constante de 2 m/s². ¿Qué tan lejos llegará al cabo de 20 s.? ¿Cuál será su velocidad final en el mismo tiempo?

Veamos los datos que tenemos:

Conocemos tres de las cinco variables, entonces, apliquemos  las  fórmulas:

Averigüemos primero la distancia que recorrerá durante los 20 segundos:

Conozcamos ahora la velocidad final del tren, transcurridos los 20 segundos:

Movimiento rectilíneo uniforme acelerado:

           

Dinámica:

El estudio de la dinámica fue iniciada por Aristóteles en torno a 384 aC. Aristóteles desarrolló una teoría en un intento de explicar los movimientos de los cuerpos. Esta teoría sigue siendo válida hasta la Edad Media, más precisamente en la época del Renacimiento. Aristóteles es considerado hoy, el precursor de Galileo Galilei, teniendo sus ideas Una de las máximas descubiertas por el antiguo pensador fue la siguiente: el movimiento puede existir sin la existencia de las fuerzas externas que actúan sobre el cuerpo. Por ejemplo, un disco de hockey cae sobre una superficie completamente lisa y en la ausencia de resistencia del aire, puede mantener su estado de movimiento de forma indefinida.

Las tres leyes son:

• Principio de Inercia o Primera Ley de Newton;
• Principio fundamental de la dinámica y la segunda ley de Newton;
• Principio de Acción y Reacción o tercera ley de Newton.
• 
  

La primera ley de Newton describe lo que ocurre con los cuerpos que están en equilibrio. La segunda ley explica lo que sucede cuando no hay equilibrio, y la tercera ley muestra que el comportamiento de las fuerzas, cuando tenemos dos cuerpos en interacción.

En el estudio del movimiento, la cinemática se propone describirlo sin preocuparse de sus causas. Cuando nos preocupamos por las causas del movimiento, estamos entrando en una zona conocida como “dinámica mecánica”.

Es por esto que Newton es considerado unos de los físicos más importantes, al igual que la dinámica, todos los paradigmas que encierra su estudio nos llevan a pensar qu eno existe un límite para la materia, en todo caso la materia limitaría nuestro pensamiento pero eso ya es algo filosófico para nuestro artículo de física.

Lo importante es saber que como Newton muchos físicos advirtieron patrones en lo referente a nuestra naturaleza, está en nosotros saber interpretar sus conclusiones y a partir de ellas comenzar a forjas las nuestras porque si no, de nada serviría.

Señalaremos algunos ejemplos de las leyes de Newton que se aplican en la vida cotidiana del ser humano

1era ley (de inercia) Por ejemplo un mozo va con una bandeja y chocas. La bandeja sigue de largo porque como sobre ella no se aplicó ninguna fuerza extra (fue sobre el mozo) tiende a seguir con la velocidad que tenía. Por supuesto que cae por la gravedad pero cae más lejos del mozo.

Se toma un cartón y pon una moneda sobre él y retira rápidamente el cartón verás que la moneda cae en el mismo lugar porque sobre ella no actuó la fuerza (fue sobre el cartón) por eso tiende a seguir quieta como estaba y no se va con el cartón sino que cae en el mismo sitio.

Cuando estás en un colectivo tiendes a irte hacia adelante cuando se frena, porqué como venías con la velocidad del micro y sobre ti no actuó ninguna fuerza tiendes a seguir con esa velocidad y te vas para adelante. Cuándo el micro arranca de nuevo te vas hacia atrás porque como estabas quieto tiendes a quedarte quieto pero el colectivo al avanzar hace que te vayas hacia atrás.

De la3era ley de Newton dentro de la dinámica te puedo contar que si yo levanto una bolsa aplicándole una fuerza ella me hace la misma fuerza a mí. Por eso me lastima los dedos.

Si una escopeta arroja un misil haciendo una fuerza que empuja al misil adelante, la escopeta recibe la misma fuerza que le hace el misil hacia atrás.

Sólo que el misil va más lejos porque tiene menos masa, la escopeta retrocede sólo un poco ya que tiene más masa que el misil.

Pues por la 2da ley de Newton la masa y la aceleración son inversamente proporcionales. Cuándo  chocas con un grandote más que tú  te vas hacia atrás y el grandote apenas se mueve.

LOGARITMO:

A los números de la sucesión primera, que es aritmética, los llamaremos logaritmos; a los de la sucesión de abajo, que es geométrica, los llamaremos antilogaritmos.

El fundador de la teoría de los logaritmos y el que les dio ese nombre fue John Napier (1550-1617). Napier, además de aficionado a las matemáticas, estaba interesado en la astrología.

Napier se dió cuenta de algo que ya conocía Arquímedes (287 a.C.-id., 212 a.C) y después Michel Stifel (1487-1567).

En cambio, Napier vio en la idea de Stifel una solución a su problema. Bastaba elegir una tabla adecuada a los números que debía utilizar. De esta manera, la segunda fila de la tabla la construyó con los senos de ángulos entre 0º y 90º y de tal manera que cada uno de los números era el anterior multiplicado por 0.9999999, y los llamó antilogaritmos. A los números de la primera fila los llamó logaritmos (los exponentes de la base para obtener la segunda fila) En 1614 publicó Mirifici logarithmorum canonis descriptio o “descripción de la maravillosa regla de los logaritmos” y hasta dos años después de su muerte no se publicó cómo fueron construidas sus tablas en la obra Mirifici logarithmorum canonis construccio (“Construcción de la maravillosa regla de los logaritmos"). Hay que señalar que Napierno concibió en los logaritmos como lo hacemos hoy en día (en resumen, representa un exponente. algo hasta simple), sino que fue algo bastante más complejo:

"El logaritmo de un seno dado es el número que aumenta aritméticamente con la misma velocidad a la que el seno ha comenzado a disminuir desde el seno dado proporcionalmente a su longitud"

Los procesos de multiplicación, división, elevación a potencias y extracción de raíces entre números reales pueden simplificarse notoriamente tal como Herry Briggs lo decía, es por esto que el uso de los logaritmos sirve hasta ahora en varias ramas y con distintas utilidades, conozcamos algunas de estas:

· El uso de logaritmo en la Tasa de Crecimiento: Un ejemplo de uso de los logaritmos es por ejemplo, si conoces la tasa de crecimiento promedio de una población, y quieres saber cuántos años tardará en llegar a cierta cantidad (por ejemplo duplicarse) necesitas el logaritmo. Para que entiendas este ejemplo, dada una población (base) y otra cantidad a la que hay que llegar (potencia), cuántas veces hay que aplicar la tasa de crecimiento (exponente) para llegar a esa cantidad; lo que necesitas obtener es el exponente, por lo que usas logaritmos.

· Uso de logaritmo en la Antropología: Pero no crean que se trata de un asunto sólo de las ciencias. Los historiadores también lo usan cuando datan la antigüedad de los restos orgánicos por el método del C14. La datación por Carbono-14 es un procedimiento para determinar la edad de ciertos objetos arqueológicos que tengan un origen biológico con una antigüedad de hasta cerca de 60.000 años. Se utiliza para fechar cosas tales como:huesos, madera, fibras vegetales que fueron creadas en un pasado relativamente reciente por actividades humanas.

· Uso de logaritmo en la escala de  Richter:  El uso del logaritmo en la escala es para reflejar la energía que se desprende en un terremoto. El logaritmo incorporado a la escala hace que los valores asignados a cada nivel aumenten de forma logarítmica, y no de forma lineal. Richter tomó la idea del uso de logaritmos en la escala de magnitud estelar, usada en la astronomía para describir el brillo de las estrellas y de otros objetos celestes.

· En la Economía: Se puede puede aplicar en la oferta y la demanda, que son de las relaciones fundamentales en cualquier análisis económico.

 · En la Banca: Se utiliza para poder medir el crecimiento de los depósitos de acuerdo al tiempo.

· En la Estadística: Su aporte es para calcular el crecimiento de una población.

· En la Biología: Puede ser utilizado para medir los efectos nutricionales de cada persona, un ejemplo es la medición de PH (es la acidez en el organismo).

· En la Geología: Se utiliza para medir o calcular tipos de fenómenos de la naturaleza como por ejemplo los sismos.

· En la Topografía: Mide la alturas de varias construcciones como por ejemplo edificios.

· En la Música: El pentagrama es una escala logarítmica que se utiliza para escribir música; la diferencia en la altura del sonido es proporcional a un logaritmo de  la frecuencia( de un DO grave a un DO siguiente más agudo , la frecuencia se dobla; es decir que la sucesión de frecuencias de las notas DO están en progresión geométrica).

· En la Publicidad: Los logaritmos se utilizan para calcular el éxito que tendrá una campaña antes de ser lanzada a los espectadores.

CONCLUSIÓN

Los logaritmos influyen mucho en nuestro día día por eso hay que comprenderlos y aprender de ellos, para poder utilizarlos mas adelante en nuestros oficios u otra cosa. 

Matemáticas:

Raíces: Una raíz corresponde a un numero que , al multiplicarse por si mismo la cantidad de veces que indique el indice, se obtiene la cantidad subradical.

Logaritmos: El logaritmo de un numero, en una base dada es el exponente al cual se debe elevar la base para obtener la cantidad.

Semejanzas: Es la variación en tamaño entre dos objetos o cuerpos pero sus formas son idénticas. 

Introducción:

En el siguiente texto representaremos lo que hemos visto en clases, practicando: raíces, logaritmos y semejanzas, ademas de ver y analizar algunos ejemplos que intervienen en la vida cotidiana.

Raíz cuadrada: (Desarrollo)

En matemáticas la raíz cuadrada o segunda raíz de una cifra numérica es aquella que al ser multiplicada por el mismo valor, el resultado es la misma cifra numérica. Es decir que si se tiene un número, y se lo descompone en su función raíz cuadrada, entonces al multiplicar esta cifra por sí misma, el resultado debería ser el primer número. Además se distingue porque la raíz cuadrada tiene un índice de numeral 2, o incluso podría representarse como un número potencial cuyo exponente sea ½ o un medio.

Las raíces cuadradas fueron uno de los primeros desarrollos de las matemáticas, siendo particularmente investigadas durante el periodo pitagórico, cuando el descubrimiento de que la raíz cuadrada de 2 era irracional (inconmensurable) o no expresable como cociente alguno, lo que supuso un hito en la historia matemática.

El símbolo de la raíz cuadrada √ fue introducido en 1525 por el matemático Christoph Rudolff para representar esta operación que aparece en su libro Coss, siendo el primer tratado de álgebra escrito en alemán vulgar. El sigo no es mas que una forma estilizada de la letra r minúscula para hacerla mas elegante, alargándola con trazo horizontal, hasta adoptar el aspecto actual, que representa la palabra latina radix que significa raíz. También se conjetura que pudiese haber surgido de la evolución que en ocaciones se usaba anteriormente para representarlo, para posteriormente se le habría añadido un trazo oblicuo en la dirección del radicando.

RAÍZ CUADRADA 

En las ciencias matemáticas,se llama raíz cuadrada de un numero a cualquier otro numero que elevado al cuadrado, es igual al primero  (√a -> b^{2 =b.b = a) es decir,} √25, numero elevado al cuadrado  5^{2= 5.5 =al primero, es decir 25.}

^{A veces se abrevia como raíz, siendo su símbolo:} √. Es la radicacion de un indice 2 o, equivalente la potenciacion con exponente. 

El concepto de raíz cuadrada puede extenderse a cualquier anillo algebraico, así es posible definir   la raiz cuadrada de algunas matrices.

                                                ¿Para que sirve la raíz cuadrada?

La industria financiera usa exponentes racionales para computar intereses, depreciaciones y otros cálculos comunes. Por ejemplo, para calcular la inflación de una casa que aumenta su valor de p1 a p2 en un período de n años, la tasa de inflación anual (expresada en decimales) es i = (p2/p1)^(1/n) -1. Para calcular el interés compuesto, la fórmula es F = P (1+i)^n, donde F es el valor del futuro y P del presente, i es la tasa de interés y n es el número de años. Si quieres calcular el interés compuesto de US$ 1000 por 18 meses a un 5 por ciento, la fórmula sería F = 1000 (1+0,05)^(3/2).

La raíz cuadrada tiene complejas e importantes aplicaciones en muchas ciencias, pero en la vida diaria la forma mas común de emplearla es en el teorema de pitagóras, que sirve para: 

*Determinar el largo de los cables que se necesitan para apuntalar una antena. 
*Saber cual es la estructura mas larga que se puede tener dentro de una bodega rectangular.
*Saber cual es el largo necesario de una viga que apuntale un marco cuadrado (para comprarla sobre medida) 
*Ay un truco para cuando no tienes una escuadra y quieres trazar una linea perpendicular a otra, tomas una cuerda y le ases 9 nudos equidistantes y unes los extremos de las cuerdas con la linea a una distancia de igual a 3 unidades de tu cuerda, tensas la cuerda en el cuarto nudo, el tramo de los 4 nudos es perpendicular a la linea gracias al teorema de pitagoras. 

                                                                                               Conclusión

En fin comprendemos que la raíz cuadrada es un ejercicio matemáticos que vamos a utilizar a lo largo de nuestra vida, en problemas que se nos aparecerán y tendremos que enfrentarlos. 

                                                                          

    

Presentacion

     

            Bienvenidos

Hola, les damos la bienvenida a este blog,  hablaremos sobre temas relacionados con la materia de Física y Matemática, con el fin de poder ayudarlos para que comprendan mejor estos temas y los apliquen en su vida cotidiana.